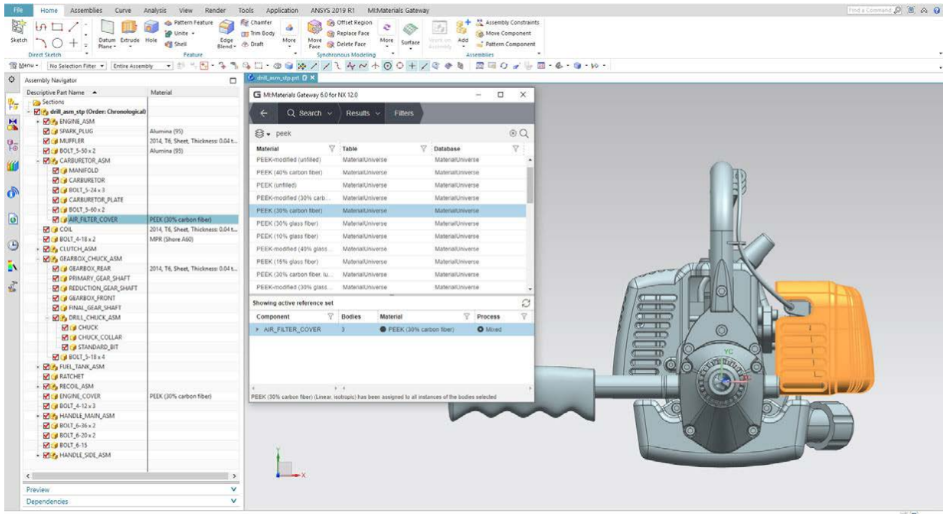
The Finite Element Method (FEM), Explained
So what exactly the Finite Element Method (FEM), and what is its relevance to engineers? For starters, to fully comprehend and quantify any physical phenomenon, such as structural or fluid behavior, thermal transport, wave propagation, or the development of biological cells, mathematics is required.
Partial differential equations (PDEs) are used to explain the majority of these processes (PDEs). However, numerical methods have been developed over the past few decades, and one of the most well-known at the moment is the finite element method, which allows a computer to solve these PDEs.
Practical Application of the Finite Element Method (FEM)
The modeling of various mechanical applications connected to aeronautical and civil engineering showed substantial promise when the finite element approach first emerged. The finite element method’s applications are just now beginning to realize their full potential.
Its potential use in linked issues such fluid-structure interaction, thermomechanical, thermochemical, and thermo-chemo-mechanical issues, biomechanics, biomedical engineering, piezoelectric, ferroelectric, and electromagnetics is among the most fascinating possibilities.
The commercial viability of the several alternative ways that have been put out in recent years has not yet been established. In other words, the impact of FEM on the engineering community is still being felt.
Partial Differential Equations and FEM
Fundamentally, it’s critical to comprehend the many PDE subgenres and how well they work with FEM. Regardless of why someone uses finite element analysis, it is crucial for everyone to comprehend this. Remembering that FEM is a tool and that any tool is only as good as its user is essential.
Three types of PDEs include elliptic, hyperbolic, and parabolic. Boundary conditions must be given, as well as possible initial circumstances, while solving these differential equations. The required inputs can be assessed based on the type of PDE. The Poisson equation (elliptic), Wave equation (hyperbolic), and Fourier law are examples of PDEs in each category (parabolic).
In order to solve elliptic PDEs, there are two primary methods: finite difference methods (FDM). In addition, variational (or energy) approaches. FEM belongs to the second group. The main tenet of many techniques is the notion of energy minimization.
Hyperbolic PDEs
Jumps in solutions are frequently related to hyperbolic PDEs. A hyperbolic PDE is the wave equation, for instance.
The original FEM technology (or Bubnov-Galerkin Method) was thought to be inadequate for solving hyperbolic PDEs because there are discontinuities (or jumps) in solutions.
However, significant improvements have been made over time to broaden the use of FEM technology.
It is important to take into account the effects of employing a numerical framework that is inappropriate for the type of PDE before wrapping up this educational blog. Such use produces what are referred to be improperly posed problems.

FEM & Establishment of Domain Parameters
This could imply that even tiny changes in the domain parameters cause significant oscillations in the solutions, or that the solutions are unreliable because they are limited to a certain region of the domain or period of time.
The definition of a well-posed explanation is one in which the defined data consistently has a single solution. Therefore, in order to examine reliability, it is crucial to find well-posed answers.
In terms of simulation software for FEM, there is really no debate. Ansys Mechanical Workbench tops the charts in all categories – from efficiency, to accuracy and affordability.